Solving application problems using similar triangles can be a daunting task for many students. However, with the right approach and techniques, it can be made easy. In this article, we will explore the concept of similar triangles, their properties, and how to apply them to solve real-world problems.
What are Similar Triangles?
Similar triangles are triangles that have the same shape, but not necessarily the same size. They have the same angle measures and proportional side lengths. In other words, if two triangles are similar, their corresponding angles are equal, and their corresponding sides are in proportion.

Properties of Similar Triangles
Similar triangles have several properties that make them useful for solving application problems. Some of the key properties include:
- Corresponding angles are equal: If two triangles are similar, their corresponding angles are equal.
- Corresponding sides are proportional: If two triangles are similar, their corresponding sides are in proportion.
- Ratio of corresponding sides is constant: If two triangles are similar, the ratio of their corresponding sides is constant.
How to Solve Application Problems Using Similar Triangles
Solving application problems using similar triangles involves several steps:
- Read the problem carefully: Read the problem carefully and identify the given information, unknown quantities, and overall objective.
- Draw a diagram: Draw a diagram to visualize the problem and identify the similar triangles.
- Identify the similar triangles: Identify the similar triangles and their corresponding angles and sides.
- Set up a proportion: Set up a proportion using the corresponding sides of the similar triangles.
- Solve the proportion: Solve the proportion to find the unknown quantity.
Examples of Application Problems
Here are a few examples of application problems that can be solved using similar triangles:
- Example 1: A ladder leaning against a wall forms a right triangle with the wall and the ground. If the ladder is 10 feet long and the distance from the base of the ladder to the wall is 6 feet, how high is the wall?
- Example 2: A tree casts a shadow of 20 feet when the angle of elevation of the sun is 30 degrees. How tall is the tree?
Step-by-Step Solution
Let's solve Example 1 step by step:
- Read the problem carefully: Read the problem carefully and identify the given information, unknown quantities, and overall objective.
- Draw a diagram: Draw a diagram to visualize the problem and identify the similar triangles.
- Identify the similar triangles: Identify the similar triangles and their corresponding angles and sides.
- Set up a proportion: Set up a proportion using the corresponding sides of the similar triangles.
Let's say the height of the wall is x feet. Then, we can set up the proportion:
6 / 10 = x / 10
- Solve the proportion: Solve the proportion to find the unknown quantity.
Cross-multiplying, we get:
6 × 10 = 10x 60 = 10x x = 6
Therefore, the height of the wall is 6 feet.

Gallery of Similar Triangles


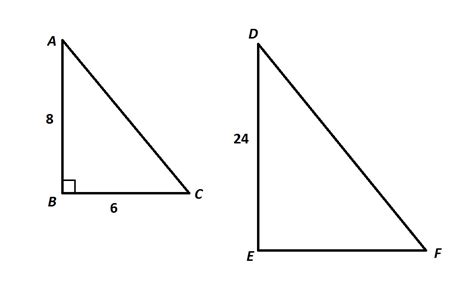

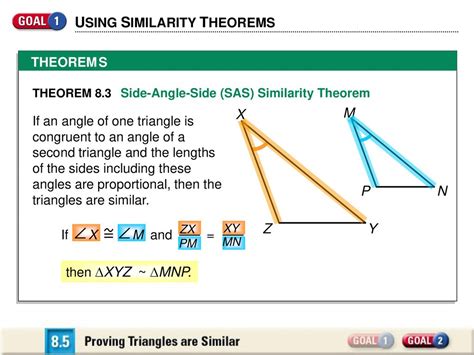
Frequently Asked Questions
What are similar triangles?
+Similar triangles are triangles that have the same shape, but not necessarily the same size. They have the same angle measures and proportional side lengths.
How do I solve application problems using similar triangles?
+To solve application problems using similar triangles, read the problem carefully, draw a diagram, identify the similar triangles, set up a proportion, and solve the proportion to find the unknown quantity.
What are the properties of similar triangles?
+Similar triangles have several properties, including corresponding angles are equal, corresponding sides are proportional, and the ratio of corresponding sides is constant.
By following these steps and understanding the properties of similar triangles, you can solve application problems with ease. Remember to always read the problem carefully, draw a diagram, and set up a proportion to find the unknown quantity. With practice and patience, you can become proficient in solving application problems using similar triangles.
